Choosing the right control valve depends on various factors. In this article, we explain the service conditions required to get a properly fitting valve, plus some supplemental conditions that result in a more accurate sizing calculation.
The following values are essential for determining which control valves are right for your application.
Liquid or gas flow rate
First and foremost, you need to distinguish the flow rate for the fluid running through your system. The flow rate for your pipeline is exactly what it sounds like — it’s the volume of fluid that passes through a given area in a given unit of time.
To determine flow rate, you need to know the area the fluid is running through and velocity of the fluid.
Inlet pressure and outlet pressure
Inlet and outlet pressure affect flow rates and are required to determine which control valve is best suited for your system.
Flowing temperature
Temperature can impact the volume and consistency of the fluid. It’s crucial to pinpoint both the operating and the relieving temperature to ensure you choose the correct control valve.
Knowing the temperature of the liquid or gas flowing through your pipes will also help determine the ideal material for your control valves. For example, steel valves can handle higher operating temperatures than valves made of either bronze or iron.
Specific gravity and mole weight
Specific gravity and mole weight are just two examples of physical properties that are critical for determining the correct valve for your application.
Specific gravity is the ratio of the substance’s density to a reference substance’s density (mass of the same unit volume). The reference substance is nearly always water for liquids and air for gases.
|
Fluid density formula (p) |
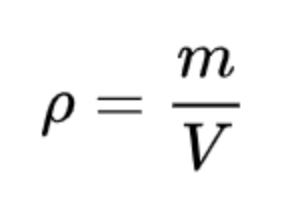 m = mass of the fluidV = infinitesimal volume |
| Unit | Water density |
| Density of water g/cm3 | 1 g/cm3 |
| Density of water g/mL | 1 g/mL |
| Density of water kg/m3 | 1000 kg/m3 |
| Density of water lb/ft3 | 62.4 lbs/ft3 |
| Unit | Approximate air density* at 59°F / 15°C |
| Density of air g/cm3 | 0.001225 g/cm3 |
| Density of air kg/m3 | 1.225 kg/m3 |
| Density of air lbm/ft3 | 0.0765 lbm/ft3 |
| Density of air slug/ft3 | 0.0023769 slug/ft3 |
*Air density decreases as altitude increases.
Mole weight (or molecular weight) refers to the mass of a molecule. It’s calculated as the sum of the mass of each constituent atom multiplied by the number of atoms of that element in the molecular formula. It may sound complicated, but with a little help from the periodic table, it’s quite simple to determine mole weight.
For example, the mole weight of water (H2O) is 18.01528 g/mol and the mole weight of carbon monoxide (CO) is 28.0101 g/mol.
The following values aren’t required for determining which control valve is right for your application, but result in a more precise sizing calculation.
Gas specific heat ratio (k)
The specific heat ratio is the ratio of the specific heat at constant pressure to specific heat at constant volume. It is sometimes also known as the isentropic expansion factor.
| Gas specific heat ratio formula |
| C = the specific heat of a gasp = refers to constant pressure conditions
v = refers to constant volume conditions |
Here are some examples of specific heat ratios:
| Specific heat ratio of various gases | ||||||||
| Gas | °F | °C | k | Gas | °F | °C | k | |
| H2 | -293.8 | −181 | 1.597 | Dry
Air |
68 | 20 | 1.40 | |
| -104.8 | −76 | 1.453 | 212 | 100 | 1.401 | |||
| 68 | 20 | 1.41 | 392 | 200 | 1.398 | |||
| 212 | 100 | 1.404 | 752 | 400 | 1.393 | |||
| 752 | 400 | 1.387 | CO2 | 32 | 0 | 1.310 | ||
| 1832 | 1000 | 1.358 | 68 | 20 | 1.30 | |||
| 3632 | 2000 | 1.318 | 212 | 100 | 1.281 | |||
| He | 68 | 20 | 1.66 | 752 | 400 | 1.235 | ||
| N2 | -293.8 | −181 | 1.47 | NH3 | 59 | 15 | 1.310 | |
| 59 | 15 | 1.404 | CO | 68 | 20 | 1.40 | ||
| Cl2 | 68 | 20 | 1.34 | -293.8 | −181 | 1.45 | ||
| Ar | -293.8 | −180 | 1.76 | O2 | -104.8 | −76 | 1.415 | |
| 68 | 20 | 1.67 | 68 | 20 | 1.40 | |||
| CH4 | -175 | −115 | 1.41 | 212 | 100 | 1.399 | ||
| -101.2 | −74 | 1.35 | 392 | 200 | 1.397 | |||
| 68 | 20 | 1.32 | 752 | 400 | 1.394 | |||
[Source]
Viscosity and pulp consistency
A fluid’s viscosity is a measure of its resistance to gradual deformation by shear stress or tensile stress and can impact flow rate. For liquids, viscosity is essentially how “thick” it is. For example, honey has a higher viscosity than water.
Flow coefficient
The flow coefficient of a valve is its capacity to allow fluid flow. It describes the relationship between the pressure drop across the valve and the corresponding flow rate.
In other words, the flow coefficient (Cv) is the volume (in US gallons) of water (at 60°F / 15.5°C) that will flow per minute through a valve with a pressure drop of 1 psi across the valve.
Note: Fisher® Controls uses different equations and expressions for liquid, steam, and gas and vapor flow coefficients, but they still have the same basic definition stated above.
| Flow Coefficient Expressions Based on Substance | |
| Liquid | Cv |
| Steam | Cs |
| Gas and vapors | Cg |
Elevation or atmospheric pressure
Varying elevations within piping systems impact the pressure at certain points. Pipe Flow Software lays out the following example on their website:
| Consider a single vertical pipe where the fluid is flowing upwards, gaining elevation height as it goes. The weight of fluid acting ‘on top’ of the fluid at a point in the pipe reduces as we consider points higher up the pipe, since there is less fluid above it. Therefore there is a loss of pressure in the pipe as the fluid rises. Conversely, at the bottom of the vertical pipe there is the full weight of fluid in the pipe ‘pushing down’ on that point and due to this, the pressure at that point increases (in comparison to the pressure on the fluid at the top of the pipe). Therefore there is a gain in pressure in the pipe as the fluid falls. |
Valve noise allowed (dBA)
Between piping, instability, and aerodynamic noise, control valves can be loud enough to make your ears ring. So when you’re on the quest for the perfect-fitting control valve, it’ll serve you well to have an idea of how loud is too loud. Proper-fitting valves with just the right design can mitigate noise.
Vapor pressure (Pv)
Vapor pressure, or equilibrium vapor pressure, is the pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases (either solid or liquid) at a given temperature in a closed system.
The equilibrium vapor pressure indicates how quickly a liquid is evaporating and relates to the tendency of particles to escape from the liquid. A substance with a high vapor pressure at normal temperatures is often referred to as volatile.
Critical pressure (Pc)
Critical pressure is the least applied pressure required at the critical temperature to liquefy a gas, or the pressure at a substance’s critical point.



